How to Implement the Binary Search Algorithm in Python

Binary search is a well-known computer science algorithm you can implement in many languages including Python.

It is an algorithm that allows finding elements in a sorted array. It is frequently brought up in programming competitions and technical interviews.

You should always use existing libraries when performing binary search in Python or any other language. We are making an exception in this tutorial so you can understand how binary search works.

To go through this tutorial you should have a basic knowledge of Python constructs and data types like tuples, lists, and dictionaries.

Let’s start!

What Is Binary Search?

The Binary search algorithm allows finding elements in a sorted array. It is more efficient than other algorithms like linear search.

For example, let’s say you have an array of ten thousand elements and you want to find the index of a specific element in the array.

Binary Search provides a very fast way to find the index of the element you want to search.

Let’s see the steps to implement binary search.

• The first step is to sort the array. Sorting means arranging the elements of the array in a certain order.
• Split the array into two halves by identifying the index of the middle element in the array.
• Compare the middle element with the value you want to find. If the element matches, then return the index of that element.
• If the value you want to find is greater than the middle element, then take the second half of the array and split it again into two halves.
• If the value you want to find is lower than the middle element, then take the first half of the array and split it into two halves.
• The process continues until the middle element matches the value you want to find.

Firstly, let’s understand what sorted means by looking at the pictures below:

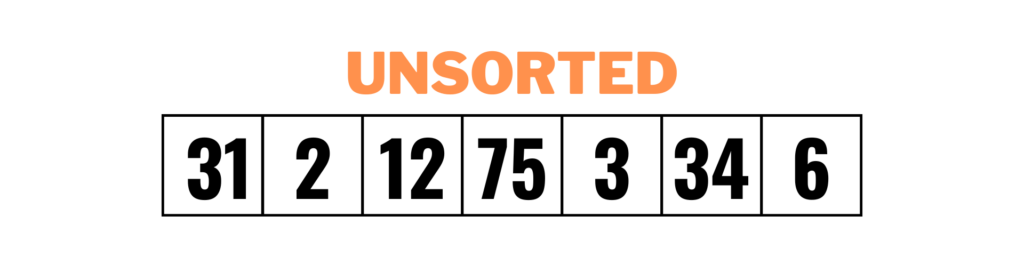
In the picture above, we have an unsorted array of integers. The first step to implementing the binary search algorithm is to sort it.

In our code examples we will store this array in a Python list:

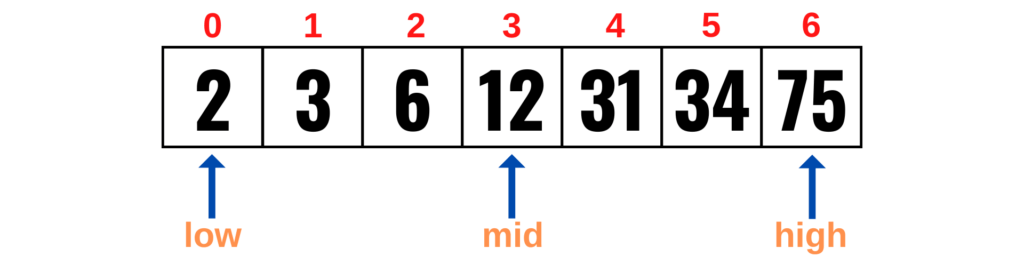
numbers = [31, 2, 12, 75, 3, 34, 6]

After sorting the list, we will define two variables: low and high.

The variable low represents index 0 in the list. The variable high represents the last index in the list.

In our case, the value of low is 0 and the value of high is 6 (the index of the last element).

Now let’s calculate the middle index of the list, using the formula below:

mid = low + (high - low) // 2

Calculate the mid index using the Python shell:

>>> low = 0
>>> high = 6
>>> mid = low + (high - low) // 2
>>> mid
3

So, the middle will be at index 3 as shown below:

Now, select an element in this list and find it using the binary search algorithm. Let’s use the number 31.

The binary search algorithm first compares the number 31 with the middle element. If they are equal, the binary search returns the index of the middle element.

if item_to_find == values[mid]:
           return mid

If the number we are searching for is greater than the mid of the list, then the low variable will move one element after the mid as shown below.

elif item_to_find > values[mid]:
            low = mid + 1

At this point, we divide the array into two halves and we compute again the right half of the array (which is greater than the mid).

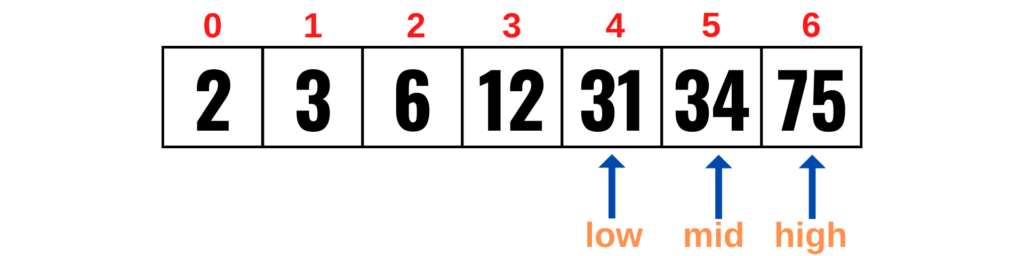
The number 31 is not equal to the mid (34), it’s actually lower than the mid so binary search sets the value of high to mid – 1.

elif item_to_find < values[mid]:
            high = mid - 1

You can see that at this point low, high, and mid are all the same number. This is the number we are looking for (31).

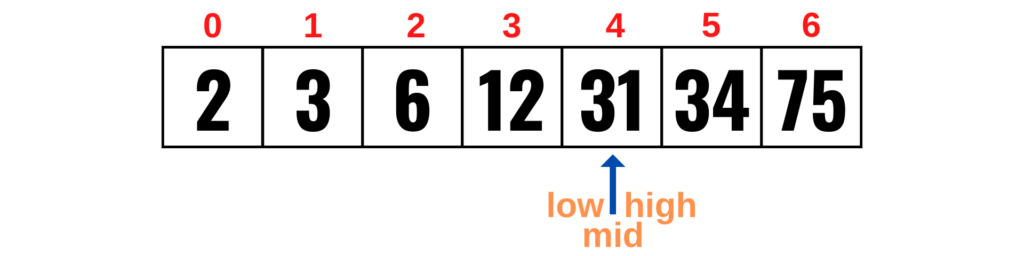
The binary search algorithm is called binary because it divides a list into two halves over and over until the value you are searching for is finally found (middle element).

In the next section, we will see how to implement the binary search algorithm using Python.

How To Implement the Binary Search Algorithm in Python

We can implement binary search in two ways:

• iterative binary search
• recursive binary search

We will see how to implement both and we will work on the sorted list.

Let’s start by implementing iterative binary search in Python which is based on a while loop.

def iterative_binary_search(low, high, values, item_to_find):
    while low <= high:
        mid = low + (high - low) // 2

        if item_to_find == values[mid]:
            return mid
        elif item_to_find < values[mid]:
            high = mid - 1
        elif item_to_find > values[mid]:
            low = mid + 1

    return -1

We have defined a function called iterative_binary_search() which takes a list and a number we want to find as parameters. We are also passing the lowest and highest indexes in the list (low and high).

The while loop is executed until the value of low is less or equal to the value of high.

In the body of the while loop, we first calculate the mid index of the list. You have already seen how the mid formula works earlier in this tutorial.

After calculating the mid index, you can use an if statement to implement the following logic:

• If the number to find is equal to the mid element of the list, we return the mid index.
• If the number to find is smaller than the mid element of the list, we split the list in half and take the left side of the list (by setting the value of high to mid – 1).
• If the number to find is greater than the mid element of the list, we split the list in half and take the right side of the list (by setting the value of low to mid + 1).

This process continues until the number you are searching for matches the element identified by the middle index.

Now let’s test our code and try to find the number 31 in our list:

if __name__ == '__main__':
    numbers = [2, 3, 6, 12, 31, 34, 75]
    number_to_find = 31

    # Executing iterative binary search
    iterative_number_index = iterative_binary_search(0, len(numbers) - 1, numbers, number_to_find)

    if iterative_number_index != -1:
        print(f"Iterative Binary Search: Number {number_to_find} found in the list at index {iterative_number_index}")
    else:
        print(f"Iterative Binary Search: Number {number_to_find} not found in the list")

The if statement on the first line is useful when you import the functions from this Python module and you don’t want to execute the code inside the if block.

To learn more about this syntax have a look at this Python article about __name__ == ‘__main__’.

When you execute this code you get the following output:

Iterative Binary Search: Number 31 found in the list at index 4

The output is correct because the index of the value we are searching for in the list is 4.

What Is Recursive Binary Search?

We can also use a recursive approach to search for any element in our Python list using binary search.

Recursion refers to the fact that our function calls itself until the value we want to find matches the value identified by the mid index.

Similarly to the previous approach, this one keeps splitting the list into small chunks until it finds the element.

Here is the recursive implementation of binary search:

def recursive_binary_search(low, high, values, item_to_find):
    if low <= high:
        mid = (low + high) // 2

        if item_to_find == values[mid]:
            return mid
        elif item_to_find < values[mid]:
            return recursive_binary_search(low, mid - 1, values, item_to_find)
        elif item_to_find > values[mid]:
            return recursive_binary_search(mid + 1, high, values, item_to_find)
    else:
        return -1

We have defined a function called recursive_binary_search() which takes a list and a number we want to find as parameters. We are also passing the lowest and highest indexes in the list (low and high).

The function calculates the mid, then:

• If the mid is equal to the number to find, the function returns the index of the middle element.
• If the number to find is lower than the middle element then the same function is called recursively by keeping the same value for low and by updating high to mid – 1.
• If the number to find is greater than the middle element then the same function is called recursively by keeping the same value for high and by updating low to mid + 1.

Notice that the updated low and high values are passed to the recursive function call.

Now we will test this code:

if __name__ == '__main__':
    numbers = [2, 3, 6, 12, 31, 34, 75]
    number_to_find = 31

    # Executing recursive binary search
    recursive_number_index = recursive_binary_search(0, len(numbers) - 1, numbers, number_to_find)

    if recursive_number_index != -1:
        print(f"Recursive Binary Search: Number {number_to_find} found in the list at index {recursive_number_index}")
    else:
        print(f"Recursive Binary Search: Number {number_to_find} not found in the list")

Let’s confirm that the output is the same as the iterative approach we used in the previous section:

Recursive Binary Search: Number 31 found in the list at index 4

The result is correct!

What Is the Time Complexity of Binary Search?

Here is the value of time complexity for the binary search algorithm in the best, average, and worst case:

• Best case: this occurs if the number you are searching for is the middle element of the sorted list. The best-case complexity of the binary search algorithm using the Big-O notation is constant and it is represented as O(1).
• Average case: the average case complexity of the binary search algorithm using the Big-O notation is logarithmic and it is represented as O(logn).
• Worst case: the worst-case complexity of the binary search algorithm using the Big-O notation is logarithmic and it is represented as O(logn).

How to Test the Binary Search Algorithm in Python

After creating our binary search functions we tested them with a single input value.

But, to make sure the way we have implemented binary search is correct, we have to test both functions with every element in our list.

We could do this manually but there is a better way…

…using the Python unittest module.

In the same directory where you have created the Python module that contains both binary search functions, create a file called test_binary_search.py.

This file will contain the code to test both binary search functions using the unittest module.

Let’s start by testing the iterative function:

import unittest
from binary_search import iterative_binary_search

class TestBinarySearch(unittest.TestCase):

    numbers = [2, 3, 6, 12, 31, 34, 75]

    def test_iterative_binary_search_with_numeric_list(self):
        self.assertEqual(iterative_binary_search(0, len(self.numbers) - 1, self.numbers, 2), 0)
        self.assertEqual(iterative_binary_search(0, len(self.numbers) - 1, self.numbers, 3), 1)
        self.assertEqual(iterative_binary_search(0, len(self.numbers) - 1, self.numbers, 6), 2)
        self.assertEqual(iterative_binary_search(0, len(self.numbers) - 1, self.numbers, 12), 3)
        self.assertEqual(iterative_binary_search(0, len(self.numbers) - 1, self.numbers, 31), 4)
        self.assertEqual(iterative_binary_search(0, len(self.numbers) - 1, self.numbers, 34), 5)
        self.assertEqual(iterative_binary_search(0, len(self.numbers) - 1, self.numbers, 75), 6)
        self.assertEqual(iterative_binary_search(0, len(self.numbers) - 1, self.numbers, 76), -1)

if __name__ == '__main__':
    unittest.main()

We have defined the TestBinarySearch class that inherits unittest.TestCase.

Then we used several assertions in the method test_iterative_binary_search_with_numeric_list() to test this algorithm against every element of our list.

Let’s execute this code:

(python-env) # python test_binary_search_iterative.py 
.
----------------------------------------------------------------------
Ran 1 test in 0.000s

OK

This test is successful!

Now add assertions to test the recursive implementation of the binary search algorithm:

import unittest
from binary_search import iterative_binary_search, recursive_binary_search

class TestBinarySearch(unittest.TestCase):

    numbers = [2, 3, 6, 12, 31, 34, 75]

    def test_iterative_binary_search_with_numeric_list(self):
        [This method doesn't change...]

    def test_recursive_binary_search_with_numeric_list(self):
        self.assertEqual(recursive_binary_search(0, len(self.numbers) - 1, self.numbers, 2), 0)
        self.assertEqual(recursive_binary_search(0, len(self.numbers) - 1, self.numbers, 3), 1)
        self.assertEqual(recursive_binary_search(0, len(self.numbers) - 1, self.numbers, 6), 2)
        self.assertEqual(recursive_binary_search(0, len(self.numbers) - 1, self.numbers, 12), 3)
        self.assertEqual(recursive_binary_search(0, len(self.numbers) - 1, self.numbers, 31), 4)
        self.assertEqual(recursive_binary_search(0, len(self.numbers) - 1, self.numbers, 34), 5)
        self.assertEqual(recursive_binary_search(0, len(self.numbers) - 1, self.numbers, 75), 6)
        self.assertEqual(recursive_binary_search(0, len(self.numbers) - 1, self.numbers, 76), -1)

if __name__ == '__main__':
    unittest.main()

Execute both tests:

(python-env) # python test_binary_search_iterative.py
..
----------------------------------------------------------------------
Ran 2 tests in 0.000s

OK

Both tests are successful!

Conclusion

The binary search algorithm is great to search for elements in sorted Python lists. The reason why this algorithm is fast is that it avoids unnecessary comparisons.

You implemented simple examples in Python that should be enough to give you an understanding of how this search algorithm works. We have covered two approaches to binary search: iterative and recursive.

And finally, you have learned how to test our two binary search functions using the Python unittest module and how time complexity applies to the binary search algorithm.

Bonus read: in this article, we have tested our functions programmatically. Learn more about testing your code using the Python unittest module.

Related course: build strong algorithm foundations with this Algorithms Specialization offered by Stanford.